Random number generators (RNGs) are a crucial part of many computational processes. As an ecologist, they are particularly important for representing the stochasticity in life in my models. The most important feature of an RNG is the ability to produce symbols or numbers which cannot be predicted better than random chance – this is surprisingly challenging for computers! RNGs can be pseudo random number generators (PRNGs), which are developed in software, or hardware random number generators (HRNGs) which are component-based and can be truly random. PRNGs use a deterministic sequence of numbers that appears random, but can be reproduced if the state of the system is entirely known.
Most PRNGs consist of a sequence of numbers which eventually repeats, but with such large periodicity that any extracted sequence of numbers will appear random. Many forms of PRNG exist, but all should involve setting the random number seed (the initial system state) and then a running an algorithm to generate the next set of random bits which can be transformed into an integer, floating point number or other data structure.
Here I introduce a few PRNGs and then compare a very basic implementation of each in terms of performance. I don’t dive into their statistical qualities at all – see other much more informed posts on that subject!
As ever, all the code is available on GitHub.
Linear congruential generator
The linear congruential generator (LCG) is one of the oldest PRNGs. The algorithm is defined by a recurrence relation,
\(X_{n+1} = (aX_n + b) mod(m)\)
where \(a\) is the “multiplier”, \(b\) is the “increment” and \(m\) is the “modulus”. If \(b=0\), and \(m\) is prime, it is known as the Lehmer RNG. Our code for an LCG is very minimal and the generator is therefore extremely fast. However, LCGs have a number of disadvantages, mainly stemming from the relatively small state space and periodicity, meaning the modulus should be at least the cube of the number of desired samples for good “randomness”. This may be fine for programming games or other applications, but for Monte Carlo simulations, where randomness is very important, this is often unacceptable.
Our C++ code for the LCG algorithm is very simple
const uint64_t modulus = static_cast<unsigned long>(pow(2, 32));
const uint64_t multiplier = 1664525;
const uint64_t increment = 1013904223;
uint64_t x;
uint64_t next()
{
x = (multiplier * x + increment) % modulus;
return x;
}
Recently, a new form of LCGs, PCGs, have gained prominence.
Mersenne Twister
Named after the Mersenne primes , the Mersenne Twister (MT) has high levels of randomness when measured by some statistical tests (but recently several issues have been exposed). It has been the de facto PRNG for many computational fields, including for Monte Carlo simulations, for some time. An adapted version of the MT is given below .
static const int N = 312;
static const int M = 156;
// constant vector a
static const uint64_t MATRIX_A = 0xB5026F5AA96619E9ULL;
// most significant w-r bits
static const uint64_t UPPER_MASK = 0xFFFFFFFF80000000ULL;
// least significant r bits
static const uint64_t LOWER_MASK = 0x7FFFFFFFULL;
// the state vector
std::array<uint64_t, N> mt_;
int mti_;
unsigned long seed;
uint64_t next()
{
static unsigned long mag01[2] = {0x0UL, MATRIX_A};
int i;
unsigned long long x;
if(mti_ >= N)
{
if(mti_ == N + 1)
init(5489ULL);
for(i = 0; i < N - M; i++)
{
x = (mt_[i] & UPPER_MASK) | (mt_[i + 1] & LOWER_MASK);
mt_[i] = mt_[i + M] ^ (x >> 1) ^ mag01[(int) (x & 1ULL)];
}
for(; i < N - 1; i++)
{
x = (mt_[i] & UPPER_MASK) | (mt_[i + 1] & LOWER_MASK);
mt_[i] = mt_[i + (M - N)] ^ (x >> 1) ^ mag01[(int) (x & 1ULL)];
}
x = (mt_[N - 1] & UPPER_MASK) | (mt_[0] & LOWER_MASK);
mt_[N - 1] = mt_[M - 1] ^ (x >> 1) ^ mag01[(int) (x & 1ULL)];
mti_ = 0;
}
x = mt_[mti_++];
x ^= (x >> 29) & 0x5555555555555555ULL;
x ^= (x << 17) & 0x71D67FFFEDA60000ULL;
x ^= (x << 37) & 0xFFF7EEE000000000ULL;
x ^= (x >> 43);
return x;
}
Xoroshiro/Xoshiro/Xorshift
A family of PRNGs use exclusive or, (XOR), shift (SHI) and bit rotation (RO) to generate random numbers. There has been some controversy recently about their statistical properties, but they appear a strong contender for a good all-rounder PRNG with excellent speed. One version, the (surprisingly short) Xoroshiro128+, is given below,
uint64_t shuffle_table[4];
// The actual algorithm
uint64_t next(void)
{
uint64_t s1 = shuffle_table[0];
uint64_t s0 = shuffle_table[1];
uint64_t result = s0 + s1;
shuffle_table[0] = s0;
s1 ^= s1 << 23;
shuffle_table[1] = s1 ^ s0 ^ (s1 >> 18) ^ (s0 >> 5);
return result;
}
SplitMix64
Another popular and very fast algorithm is the SplitMix64. It is the default in some languages (although many more use MT-based PRNGs by default). Again, the code is surprisingly minimal.
uint64_t x{}; /* The state can be seeded with any value. */
uint64_t next()
{
uint64_t z = (x += UINT64_C(0x9E3779B97F4A7C15));
z = (z ^ (z >> 30)) * UINT64_C(0xBF58476D1CE4E5B9);
z = (z ^ (z >> 27)) * UINT64_C(0x94D049BB133111EB);
return z ^ (z >> 31);
}
So which is fastest?
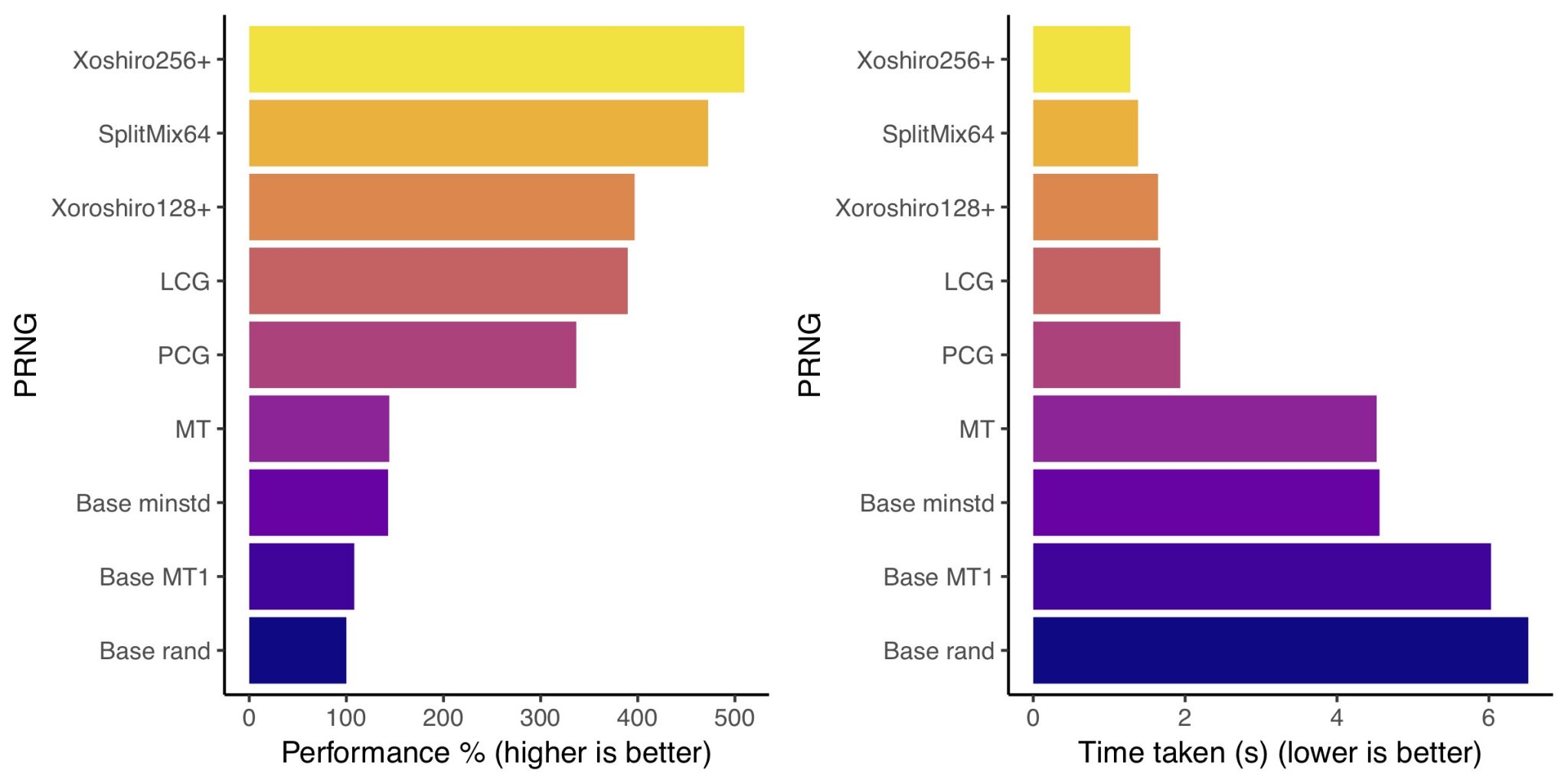
Performance is only one important feature of PRNGs, but is crucial to many use cases. I tested custom implementations of a few PRNGs adapted from various versions across the internet, plus a few of the in-built C++ algorithms for comparison. Note that below the base MT implementation and PCG generate 32 instead of 64 bit ints. Timings were tested over 109 random numbers on an 2.6 GH Ivy Bridge i7 laptop processor. Don’t take these numbers as gospel – perform your own tests if speed is important!
The Xoshiro256+ PRNG comes out on top, closely followed by SplitMix64. The rest of the pack aren’t too far behind, with the base implementations and MT being considerably slower.
Comparing against the baseline of the slowest PRNG (the base rand implementation) we see a 5x performance increase from moving to the fastest Xoshiro256+ PRNG.
Which PRNG should I use?
All methods have their drawbacks, either in speed or different deficits in statistical “randomness”. There are many online articles (see here, here and here) which discuss the various advantages and disadvantages of particular methods. Personally, I’m going to use the Xoshiro256+ algorithm, because it seems really fast and its statistical issues don’t matter (at least not obviously) to my work. Otherwise, I’d probably go for one of the PCG methods which have generated a lot of noise recently, and probably there are faster versions than the one I used here available. Check them out here.
2 thoughts on “Random number generators for C++ performance tested”
> Otherwise, I’d probably go for one of the PCG methods which have generated a lot of noise recently
The PCG methods have only “generated a lot of noise” because their author has promoted them heavily. The author has not subjected them successfully to any kind of rigorous peer review, and has acted strangely to say the least. I would not trust them.
I’m less skeptical of PCG than Foo. Review means that competent people have studied it and looked for flaws, and that has happened despite being only a technical report.
O’Neill very much did submit it for formal review and publication, specifically to ACM Transactions on Mathematical Software (TOMS), where the reviewers felt that the paper was overall good but too long for the journal and and not a good fit for its subject matter.
While this procedural rejection may have led to a less rigorous review of the technical content, the parts that were found wanting were relatively minor areas (additional references to previous work, exposition, terminology, etc.).
The main criticism has come from Vigna, but having looked at his complaints I do not find them persuasive. He prefers the LFSR construction. Which is reasonable, but LFSRs have their own problems, as O’Neill (and others) have documented in turn.
I note that Blackman & Vigna’s key paper on the Xoshiro family “Scrambled linear pseudorandom number generators” was submitted to the same journal in 2018 or 2019 (his bibliography page lists it as “to appear in ACM Trans. Math. Softw.”) and has *also* not been published there.
I’d call that a dead heat in the formal review department.
What I’m curious about is some other fast generators that were not included:
* Multiply with carry
* Doty-Humphrey’s SFC generators
* Jenkins’ JSF and WOB2M generators
* Other generators from the PractRand suite